In Hermite-Einstein Metrics and Stability we talked about Hermite-Einstein metrics. These are metrics on a holomorphic vector bundle $E$ that satisfy an analogous condition with the Einstein condition on a Riemannian manifold. This time we will specialize in the case where $E$ is the holomorphic tangent bundle $TX$.
Specializing to the holomorphic tangent bundle $TX$ imposes a significantly more restrictive interpretation of the Hermite-Einstein condition. Any Hermitian metric $g$ on the complex manifold $X$ induces a Hermitian metric on the holomorphic tangent bundle $TX$. Thus it would not be very natural to try and seek for another unrelated Hermitian metric on $TX$. Recall that the Hermite-Einstein condition intertwines the Hermitian metric on $X$ with the Hermitian metric on $E$.
A Hermitian manifold $(X,g)$ is called Kähler-Einstein if $(X,g)$ is Kähler and the naturally induced Hermitian metric on the holomorphic tangent bundle is Hermite-Einstein. In this case, the metric $g$ is Kähler-Einstein. If a Kähler-Einstein metric $g$ on $X$ exists, the complex manifold $X$ is also called a Kähler-Einstein manifold.
Explicitly, the above definition means that the curvature of the Levi-Civita connection satisfies
\[i\Lambda_\omega F_\nabla = \lambda\operatorname{id}_{TX}.\]
Usually the Kähler-Einstein condition is introduced via the Ricci curvature. It is not too difficult to see that the definition we gave is equivalent to
\[\operatorname{Ric} = \lambda \omega.\]
The reason we require $X$ to be Kähler is due to the two following propositions.
Let $\widetilde{\nabla}$ be the Levi-Civita connection on the Riemannian manifold $(X,g)$ and assume that the complex structure $J$ is parallel.
-
Under the isomorphism $TX \cong T^{1,0}X$, the connection $\widetilde{\nabla}$ induces the Chern connection $\nabla$ on the holomorphic tangent bundle $T^{1,0}X$.
-
The manifold is Kähler and the Kähler form $\omega$ is parallel.
-
Since $J$ is parallel, we obtain a connection $\nabla$ on the complex vector bundle $T^{1,0}X$. The connection is Hermitian if and only if $dg_{\Bbb C}(u,v) = g_\Bbb C(\nabla u, v) + g_\Bbb C(u,\nabla v)$. Since the Levi-Civita connection is a metric connection, both sides of the real parts of the equation are equal. The imaginary parts are up to a factor $d\omega(u,v) = dg(J(u), v)$ respectively $g(J(\widetilde{\nabla}u), v) + g(J(u), \widetilde{\nabla}v)$. Using the fact that $\widetilde{\nabla}J = J\widetilde{\nabla}$, one sees that these also coincide. Since the Levi-Civita connection is torsion free we conclude the result.
-
Since $\widetilde{\nabla}$ is a torsion-free connection on the Riemannian manifold $(X,g)$, any $\widetilde{\nabla}$-parallel form is closed. It suffices to show that $\omega$ is parallel. We have that
$$
\begin{align*}
(\widetilde{\nabla}\omega)(u,v) &= d(\omega(u,v)) - \omega(\widetilde{\nabla}u, v) - \omega(u, \widetilde{\nabla}v) \\
&= d(g(Ju,v)) - g(\widetilde{\nabla}J(u),v) - g(J(u), \widetilde{\nabla}v) \\
&= 0
\end{align*}
$$
since $\widetilde{\nabla}$ is a metric connection.
As a partial converse of the above proposition we have:
Let $(X,g)$ be a Kähler manifold. Then under the isomorphism $TX \cong T^{1,0}X$ the Chern connection $\nabla$ on the holomorphic tangent bundle $T^{1,0}X$ corresponds to the Levi-Civita connection $\widetilde{\nabla}$.
To prove this one needs to show that under the assumption that $(X,g)$ is Kähler, the Chern connection is torsion-free. Locally
$$
\omega = \frac{1}{2}h_{ij} dz^i \wedge d\bar{z}^j
$$
and
$$
A = (h_{ji})^{-1}(\partial h_{ji})
$$
for the connection form. The fundamental form is Kähler if and only if $\frac{\partial h_{ij}}{\partial z_k} = \frac{\partial h_{kj}}{\partial z_i}$ and the latter symmetry condition yields that the Chern connection is torsion-free.
Some elementary examples of Kähler-Einstein manifolds are, for example, the projective space, complex torus, and ball quotients.
Recall that in Riemannian geometry if $(M,g)$ is a Riemannian manifold, then for any $p \in M$ and linearly independent vectors $v,w \in T_pM$ the sectional curvature of the plane $\Pi$ spanned by $v$ and $w$ is given by
\[K(\Pi) = \frac{R_p(v,w,w,v)}{|v\wedge w|^2},\]
where $|v\wedge w|^2 = \sqrt{|v|^2|w|^2 - \langle v,w\rangle^2}$. If the vectors $v$ and $w$ are orthonormal we have
\[K(\Pi) = R_p(v,w,w,v).\]
Also note that the Gaussian curvature given by $K = \frac{1}{2}S$, where $S$ is the scalar curvature is an intrinsic invariant of $M$. For the geometric picture, if $V \subset T_pM$ is a star-shaped neighborhood of zero on which $\exp_p$ is a diffeomorphism onto its image, then $\Pi \cap V$ is an embedded $2$-dimensional submanifold of $V$. It follows that $S_\Pi = \exp_p(\Pi \cap V)$ is an embedded $2$-dimensional submanifold of $M$ containing $p$. The sectional curvature $K(\Pi)$ is then just the intrinsic Gaussian curvature at $p$ of the surface $S_\Pi$ with the induced metric from the embedding $S_\Pi \subset M$.
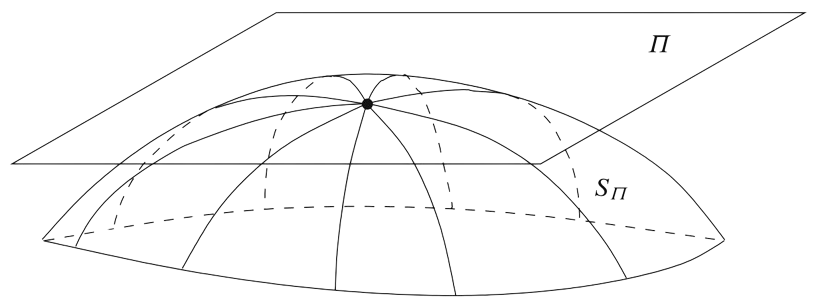
In the Kähler case, we consider something called holomorphic sectional curvature.
Let $(X,g)$ be a Kähler manifold, and let $J$ be the complex structure. For any $p \in X$ and any $2$-dimensional $\Bbb R$-subspace $\Pi$ of the $\Bbb C$-vector space $T_pX$ with $J_p(\Pi) \subset \Pi$, the holomorphic sectional curvature along $\Pi$ is defined by
$$
K(\Pi) = R(\xi, J\xi, \xi, J\xi),
$$
where $\xi$ is a unit vector in $\Pi$.
Let $(X,g)$ be a Kähler manifold. Then the following are equivalent:
-
$X$ has a constant holomorphic sectional curvature $\kappa$.
-
For any $X,Y,Z,W \in TX$ we have
$$
\begin{align*}
R(X,Y,Z,W) &= -\frac{\kappa}{4}(g(X,W)g(Y,Z)-g(X,Z)g(Y,W) \\
&+ g(X,JW)g(Y,JZ) - g(X,JZ)g(Y,JW) + 2g(X,JY)g(W,JZ) ).
\end{align*}
$$
Analogously as in the Riemannian case, Kähler manifolds with constant holomorphic sectional curvature are Kähler-Einstein.
Let $(X,g)$ be a Kähler manifold with constant holomorphic sectional curvature $\kappa$. Then $(X,g)$ is Kähler-Einstein with constant $\lambda = \frac{\kappa(n+1)}{2}$.
Let $e_1,J(e_1),\dots,e_{2n-1}, J(e_{2n})$ be an orthonormal basis of $TX$. We have that
$$
\begin{align*}
\operatorname{Ric}(X,Y) &= \sum R(e_i,X,e_i,Y) + \sum R(Je_i,X,Je_i,Y) \\
&= \frac{\kappa}{4} \sum (g(X,Y)-g(X,e_i)g(Y,e_i) + 3g(X,Je_i)g(Y,Je_i)) \\
&+ \frac{\kappa}{4} \sum (g(X,Y)-g(X,Je_i)g(Y,Je_i) + 3g(X,e_i)g(Y,e_i)) \\
&= \sum \frac{\kappa}{2}(g(X,Y) + g(X,e_i)g(Y,e_i) + g(X,Je_i)g(Y,Je_i)) \\
&= \frac{\kappa(n+1)}{2}g(X,Y).
\end{align*}
$$
Let’s then discuss the Uniformization Theorem. In a sense this is just generalization upon generalization on the Riemann mapping theorem. The uniformization theorem for Riemann-surfaces can be thought of as a generalization of the Riemann mapping theorem and it states that every simply connected Riemann-surface is conformally equivalent to one of the three surfaces: the open unit disc, the complex plane, or $\Bbb CP^1$. The uniformization theorem gives a similar classification for complete Kähler manifolds of constant holomorphic sectional curvature.
Let $(X,g)$ be a complete Kähler manifold of constant holomorphic sectional curvature $R_{i\bar{j}k\bar{l}} = \lambda(g_{i\bar{j}}g_{k\bar{l}} + g_{i\bar{l}}g_{k\bar{j}})$ for some constant $\lambda$. Then its universal cover $\widetilde{X}$ is one of the three spaces: $B^n, \Bbb C^n$, or $\Bbb CP^n$.
Note that in the cases $\Bbb C^n$ has a vanishing holomorphic sectional curvature and $B^n$ as well as $\Bbb CP^n$ have $\lambda = -1$ and $\lambda < 0$ respectively. After appropriate rescaling we have three cases to consider, $\lambda = -1, \lambda = 0$ and $\lambda = 1$. Let's first consider the cases $\lambda \le 0$. Let $(X_\lambda,g_\lambda)$ be the Kähler manifold of constant holomorphic sectional curvature $\lambda$ as in the above cases. Consider the exponential maps $\exp_0 : T_0X_\lambda \to X_\lambda$ and $\exp_p : T_p\widetilde{X} \to \widetilde{X}$. The sectional curvatures of $X_\lambda$ and $\widetilde{X}$ are non-positive and by the Cartan-Hadamard theorem, the exponential maps are diffeomorphisms. Identify both $T_0X_\lambda$ and $T_p\widetilde{X}$ with $\Bbb R^{2n}$ and define the map
$$
\varphi = \exp_p \circ \exp_0^{-1}.
$$
We claim that $\varphi$ is an isometry and once this is proved, we have proved the theorem. By Cartan-Hadamard, for any $x \in X_\lambda$ and $Y \in T_xX_\lambda$, there exists $v,w \in \Bbb R^{2n}$ such that $\exp_0(v) = x$ and $d\exp_0(v)(w) = Y$. If $q = \varphi(x), \widetilde{Y} = d\varphi(Y)$, then $\exp_p(v) = q$ and $d\exp_p(v)(w) = \widetilde{Y}$. Set $\gamma(s,t) = \exp_0(s(v+tw))$ and let $J$ be the corresponding Jacobi field. Then $J(1) = Y$ and we have that
$$
\nabla_{\dot{\gamma}}\nabla_{\dot{\gamma}}J - R(\dot{\gamma},J)\dot{\gamma} = 0.
$$
Fix an orthonormal basis $e_1,\dots,e_{2n}$ for $T_0X_\lambda$ such that $e_1 = \frac{\dot{\gamma}}{|\dot{\gamma}|}$ and $e_{n+i} = Je_i$. Parallel transport this basis along $\gamma$, then $\nabla_{\dot{\gamma}}e_i(s) = 0$ and $e_i(0)=e_i$. Write $J(s) = J^i(s)e_i(s)$, then
$$
\frac{\partial^2J^i(s)}{\partial^2 s} - |\dot{\gamma}|\langle R(e_i,e_k)e_1,e_1\rangle J^k(s) = 0.
$$
Since
$$
\langle R(e_i,e_k)e_1,e_1\rangle = \frac{\lambda}{4}(\delta_{ik}-\delta_{1i}\delta_{1k}- \delta_{1,i-n}\delta_{k,n+1}+ 2\delta_{1,i-n}\delta_{1,k-n})
$$
we conclude that $Y$ is uniquely determined by $v,w$ and $\lambda$. Since $\widetilde{Y}$ satisfies the same equation with the same initial values, we have $|\widetilde{Y}| = |Y|$. That is $\varphi$ is an isometry. If $\lambda > 0$, then the Ricci curvature is positive and by Myers' Theorem, we know that $\widetilde{X}$ is compact. Let $U_0 \subset \Bbb CP^n$ be the open set given by $z_0 \ne 0$. Then by the same argument, we can show that $\varphi$ is an
isometry from $U_0$ onto its image. Since $U_0$ is dense in $\Bbb CP^n$ and $\widetilde{X}$ is compact, we can extend $\varphi$ to all of $\Bbb CP^n$ so that $\varphi$ remains an isometry.
Lastly, we’ll discuss the uniformization for Kähler-Einstein manifolds. This is a theorem we are going to need in an upcoming post on Calabi-Yau manifolds.
Let $(X,g)$ be a Kähler-Einstein manifold. Then $\widetilde{X} \cong \Bbb CP^n, \Bbb C^n$ or $B^n$ if and only if
$$
\left(2(n+1)c_2(X) - nc_1(X)^2\right)\wedge [\omega]^{n-2} = 0.
$$
Here $\cong$ means isometric up to scaling.
By the uniformization theorem for Kähler manifolds, it suffices to prove that the equality is equivalent to $X$ being a manifold of constant holomorphic sectional curvature. Recall that
$$
\det\left(I + t\frac{i}{2\pi}\Omega\right) = I + tf_1(\Omega) + t^2f_2(\Omega) + \dots,
$$
where $\Omega$ is the curvature matrix and the $f_i$'s represent the Chern classes of $X$. Now
$$
f_1(\Omega) = \operatorname{tr}\left(\frac{i}{2\pi} \Omega\right)
$$
and
$$
f_2(\Omega) = \frac{1}{8\pi^2}(\operatorname{tr}(\Omega \wedge \Omega) - \operatorname{tr}(\Omega)^2).
$$
These give
$$
f_1(\Omega)^2 - 2f_2(\Omega) = \left(\frac{i}{2\pi}\right)^2 \operatorname{tr}(\Omega \wedge \Omega).
$$
Thus
$$
(c_1(X)^2 - 2c_2(X))\wedge [\omega]^{n-2} = \left(\frac{i}{2\pi}\right)^2 \int_X \operatorname{tr}(\Omega \wedge \Omega) \wedge \omega^{n-2}.
$$
We'll denote by $R^\circ$, the traceless part of the curvature $R$ corresponding to $g$. The Kähler-Einstein condition gives $\operatorname{Ric} = \lambda\omega$ and so locally
$$
R^\circ_{i\bar{j}k\bar{l}} = R_{i\bar{j}k\bar{l}}-\frac{\lambda}{n+1}(g_{i\bar{j}}g_{k\bar{l}}+g_{i\bar{l}}g_{k\bar{j}}).
$$
The tensor $R^\circ$ now measures how much the metric deviates from having constant sectional curvature. It suffices thus to show that $R^\circ = 0$ is equivalent to the equality given in the statement of the theorem. We have that
$$
\frac{1}{n(n-1)}|R^\circ|^2\omega^n = -\left(\frac{i}{2}\right)^2 \operatorname{tr}(\Omega \wedge \Omega) \wedge \omega^{n-2} + \frac{\lambda^2}{n+1}\omega^n.
$$
It follows that
$$
\pi^2(c_1(X)^2 - 2c_2(X))\wedge [\omega]^{n-2} = \int_X \frac{\lambda^2}{n+1}\omega^n - \frac{1}{n(n-1)}\int_X |R^\circ|^2\omega^n.
$$
Also $\int_X \lambda^2\omega^n = \pi^2c_1(X)^2\wedge [\omega]^{n-2}$ and so
$$
\frac{n\pi^2}{n+1}\left(c_1(X)^2 - \frac{2(n+1)}{n}c_2(X)\right)\wedge [\omega]^{n-2} = -\frac{1}{n(n-1)}\int_X |R^\circ|^2\omega^n.
$$
Thus $X$ is of constant holomorphic sectional curvature if and only if
$$
\left(nc_1(X)^2-2(n+1)c_2(X)\right)\wedge [\omega]^{n-2} = 0.
$$
More generally, this shows that for any Kähler-Einstein manifolds, not necessarily of constant holomorphic sectional curvature, the following inequality holds
$$
\left(nc_1(X)^2-2(n+1)c_2(X)\right)\wedge [\omega]^{n-2} \le 0.
$$
